Imagine uma floresta antiga à luz fraca de uma noite de verão. À medida que os últimos raios do sol desaparecem no horizonte, um pequeno flash chama sua atenção.
Você se vira, prende a respiração; ele pisca novamente, pairando a cerca de 60 cm acima da serapilheira. Do outro lado da clareira escura, uma resposta fugaz. Depois outro, e outro, e em poucos minutos vaga-lumes se espalharam por toda a floresta silenciosa.
A princípio, eles parecem desorganizados. Mas logo aparecem alguns pares coordenados, pequenos conjuntos piscando no mesmo tempo duas vezes por segundo. Os pares se fundem em tríades, quíntuplos e, de repente, toda a floresta está pulsando com uma batida comum e brilhante. O enxame atingiu a sincronia.
As congregações de vaga-lumes estão se espalhando em eventos de encontros rápidos. Os flashes transmitem um diálogo de namoro entre `machos publicitários´ e `fêmeas seletivas´. Moldados pela interação de competição e cooperação entre milhares de vaga-lumes, surgem padrões de luz coletivos, análogos cintilantes aos murmúrios de bandos de pássaros voando juntos. O misterioso fenômeno da sincronização do flash de alguns vaga-lumes tem intrigado os cientistas por mais de um século.
A sincronia é onipresente em todo o universo, desde nuvens de elétrons até ciclos biológicos e órbitas planetárias. Mas a sincronia é um conceito complexo com muitas ramificações. Abrange várias formas e, geralmente são reveladas pela matemática e posteriormente exploradas na natureza.
Pegue o enxame de vaga-lumes. Espere um pouco mais e entre o refrão iluminado, outra coisa aparece: Alguns pisca-piscas discordantes se separam e continuam fora do compasso. Eles piscam no mesmo ritmo, mas mantêm um atraso resoluto com seus pares conformistas. Isso poderia ser evidência de um fenômeno previsto por equações matemáticas, mas nunca antes visto na natureza?
Sincronia, com uma reviravolta
Vinte anos atrás, enquanto se aprofundavam nas equações que formam a estrutura da sincronia, os físicos Dorjsuren Battogtokh e Yoshiki Kuramoto notaram algo peculiar. Sob circunstâncias específicas, suas soluções matemáticas descreveriam um conjunto ambivalente, mostrando sincronia generalizada intercalada com alguns constituintes erráticos e flutuantes.
Seu modelo baseava-se em uma coleção de relógios abstratos, chamados osciladores, que tendem a se alinhar com seus vizinhos. O estado não uniforme foi surpreendente, porque as equações assumiram que todos os osciladores eram perfeitamente idênticos e conectados de forma semelhante aos outros.
A quebra espontânea da simetria subjacente é algo que normalmente incomoda os físicos. Acalentamos a ideia de que alguma ordem no tecido de um sistema deve se traduzir em ordem semelhante em sua dinâmica em larga escala. Se os osciladores forem indistinguíveis, eles devem entrar em sincronia ou permanecer caóticos – sem mostrar comportamentos diferenciados.
Isso despertou a curiosidade de muitos, incluindo os matemáticos Daniel Abrams e Steven Strogatz, que batizaram o fenômeno de “quimera”. Na mitologia grega, a Quimera era um monstro híbrido feito de partes de animais incongruentes – portanto, um nome adequado para uma miscelânea de aglomerados de osciladores incompatíveis.
A princípio, as quimeras eram raras em modelos matemáticos, exigindo um conjunto muito específico de parâmetros para se materializar. Com o tempo, aprendendo onde procurar, os teóricos começaram a descobri-las em muitas variações desses modelos, apelidando-as de “respiração”, “torcidos”, “multicabeças” e outros epítetos misteriosos. Ainda assim, permaneceu misterioso se essas quimeras teóricas também eram possíveis no mundo físico – ou apenas um mito matemático.
Uma década depois, alguns experimentos engenhosos montados em laboratórios de física produziram as esquivas quimeras. Eles envolviam redes de interações finamente ajustadas entre osciladores sofisticados. Enquanto provavam que projetar a coexistência de coerência e incoerência era um empreendimento delicado, mas possível, eles deixaram a questão mais profunda sem resposta: as quimeras matemáticas também poderiam existir no mundo natural?
Descobriu-se que seria necessário um minúsculo inseto luminescente para clarear a questão.

Quimera em meio ao coro piscante dos vaga-lumes
Como pós-doutorando no Laboratório Peleg da Universidade do Colorado, trabalho para decifrar o funcionamento interno dos enxames de vaga-lumes. Nossa abordagem se baseia em um nicho pouco conhecido da física moderna: o comportamento coletivo animal. Simplificando, o objetivo geral é revelar e caracterizar padrões de larga escala espontâneos e não supervisionados na dinâmica de grupos de animais. Em seguida, investigamos como esses padrões auto organizados emergem das interações individuais.
Aconselhados por especialistas em vaga-lumes, meus colegas e eu atravessamos o país até o Parque Nacional Congaree, na Carolina do Sul, para perseguir os Photuris frontalis, uma das poucas espécies norte-americanas conhecidas por sincronizar. Instalamos nossas câmeras em uma pequena clareira na floresta entre os pinheiros loblolly. Logo depois que as primeiras tremulações apareceram no crepúsculo, observamos uma sincronia muito rítmica e precisa, aparentemente tão limpa quanto previsto pelas equações.
Esta foi uma experiência encantadora, mas que me deixou reflexivo. Preocupava-me que essa exibição fosse ordenada demais para nos permitir inferir qualquer coisa a partir dela. Os físicos aprendem sobre as coisas observando suas flutuações naturais. Aqui, parecia haver pouca variabilidade para investigar.
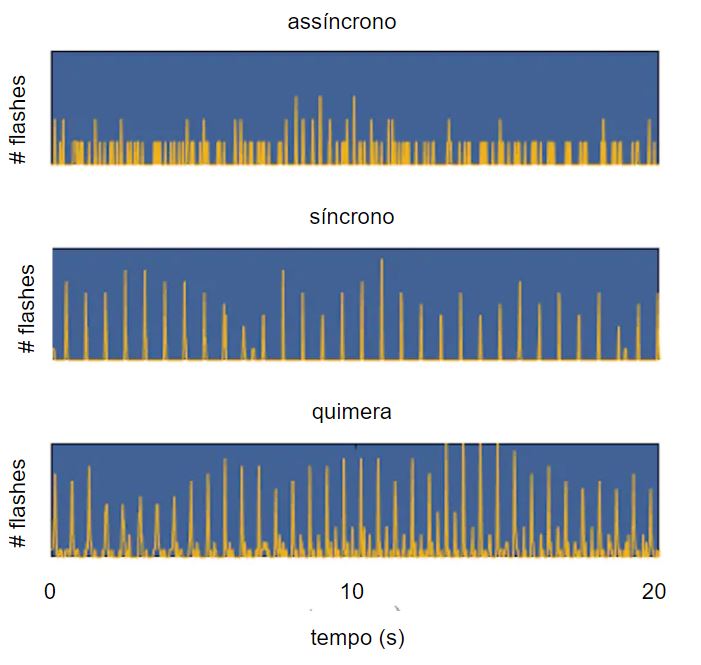
A sincronia se manifesta nos dados na forma de picos agudos no gráfico do número de flashes ao longo do tempo. Esses picos indicam que a maioria dos flashes ocorre no mesmo instante. Quando não o fazem, o traço parece irregular, como rabiscos. Em nossos enredos, primeiro não vi nada além do padrão perfeito de sincronia impecável.
Acontece que a quimera estava escondida à vista de todos, mas eu tive que vagar mais pelos dados para encontrá-la. Lá, entre os picos do coro leve, alguns picos mais curtos indicavam facções menores em sincronia entre si, mas não com o grupo principal. Eu os chamei de “personagens”. Juntamente com o refrão sincronizado, esses personagens incongruentes compõem a quimera.
Como no antigo teatro grego, o coro define o pano de fundo enquanto os personagens criam a ação. Os dois grupos estão interligados, percorrendo o mesmo palco, como revelamos a partir da reconstrução tridimensional do enxame. Apesar da divisão em seu ritmo, suas dinâmicas espaciais parecem indistinguíveis. Os personagens não parecem se reunir ou seguir um ao outro.
Essa auto-organização inesperadamente misturada levanta ainda mais questões. Os personagens do enxame decidem conscientemente se separar, talvez para sinalizar sua emancipação? Ou eles se encontram espontaneamente presos fora do ritmo? As descobertas matemáticas podem esclarecer a dinâmica social em jogo entre os besouros luminosos?
Ao contrário dos osciladores abstratos em equações matemáticas, os vaga-lumes são seres cognitivos. Eles incorporam informações sensoriais complexas e as processam por meio de um canal de tomada de decisão. Eles também estão constantemente em movimento, formando e quebrando laços visuais com seus pares. Modelos matemáticos simplificados ainda não capturam essas complexidades.
Na floresta silenciosa, os flashes sincronizados e suas contrapartes dissonantes podem ter iluminado um tesouro de novas quimeras para os matemáticos e os físicos perseguirem.
Fonte: The Conversation / Raphael Sarfati
Tradução: Redação Ambientebrasil / Maria Beatriz Ayello Leite
Para ler a reportagem original em inglês acesse: https://theconversation.com/synchrony-with-chaos-blinking-lights-of-a-firefly-swarm-embody-in-nature-what-mathematics-predicted-193984




